Electro-Optical Effect and Crystals

BBO,   KTP,   KD*P,  LN, RTP crystals for E-O

When an electric field (E) is applied to an electro-optic (E-O) crystal, the refractive index of the crystal changes linearly to the electric field. The phenomenon is called linear electro-optic effect. In KD*P crystal, as an example, the change of the refractive index is Δn = 0.5no3γ₆₃E if both the light propagation and the electric field are along the z-axis, where no is refractive index without electric field and γ63 the electro-optic coefficient of KD*P.   

When a linearly polarized light passes through an E-O crystal, the phase retardation (Γ ) is induced by Δn, i.e. Γ = 2πΔnL/λ,  where L is the crystal length, λ the light wavelength. For KD*P, again as an example, the phase retardation can be expressed as Γ = πLno3 γ63E/λ. Apparently the phase of light changes with electric field E. This is called E-O phase modulation. Further, if two polarizers with orthogonal polarizations are placed at the input and output ends of an E-O crystal, the output intensity of light will be I = I0 sin2(Γ/2), where I0 is the input intensity. The intensity of light then can be modulated by electric field. This is E-O amplitude modulation.

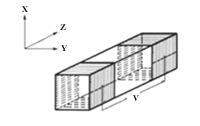
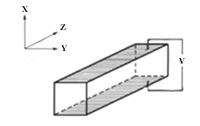
There are two types of E-O modulations,

(1) Longitudinal E-O modulation where the directions of electric field and light propagation are the same. The KDP isomorphic crystals are normally used in this scheme.

(2) Transverse E-O modulation where the directions of electric field and light propagation are perpendicular to each other. LiNbO3, MgO:LiNbO3, ZnO:LiNbO3, BBO and KTP crystals are usually employed in this scheme.